Other news

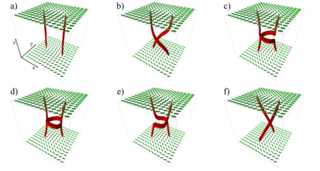
Samo Kralj from the Department of Solid State Physics F5 and colleagues from Faculty of Mathematics and Physics, University of Ljubljana and Case Western Reserve University, Cleveland published an article in the journal Crystals with the title Reconfiguration of nematic disclinations in plane-parallel confinements.

They study numerically the reconfiguration process of colliding |m|=1/2 strength disclinations in a nematic liquid crystal (NLC). A Landau-de Gennes approach in terms of a tensor nematic order parameters is used. Initially, different pairs of parallel wedge disclinations were formed connecting opposite substrates confining the NLC in a plane-parallel cell. The collisions are triggered by the relative rotation of the azimuthal angle of the substrates that strongly pin the defect end points. They illustrate qualitatively different rewiring processes.

Amid Ranjkesh, Samo Kralj in Aleksander Zidanšek  from the Department of Condensed Matter Physics F5 and colleagues from Faculty of Natural Sciences and Mathematics, University of Maribor and Jožef Stefan International Postgraduate School have published a paper in  Front. Soft. Matter with the tittle Phase behavior of nematic-nanoparticle mixtures.

We study the effects of nanoparticles (NPs) on thermotropic nematic liquid crystals (LCs) in relatively dilute NP–LC mixtures. We are interested in the fundamental generic mechanisms that quantitatively and qualitatively affect the phase behavior of LCs. A simple molecular field analysis shows that a phase transition will likely occur upon entry into the ordered phase. Moreover, the interaction between nematogenic NPs and LCs could force a sergeant–soldier-like behavior, in which only the phase behavior of one component is affected despite the symmetric appearance of the coupling term. When NPs are anisotropic, their influence on LC phase behavior can be qualitatively different depending on the anchoring, even in the absence of the disorder. We illustrate numerically that a random-field-type disorder might impose either short-range, quasi-long-range, or even long-range order, which might survive.