EMP 2022/2023

(2. 10. 2023)

Naloge in rešitve vseh pisnih izpitov v študijskem letu 2022/2023

(1. 9. 2023)

3. pisni izpit: naloge, REŠITVE in REZULTATI

V priloženih dokumentih objavljam naloge, rešitve nalog (s točkovalnikom) in tabelo rezultatov 3. pisnega izpita skupaj z ocenami po 3. pisnem izpitu. Kot ponavadi, stolpci n1p, n2p in n3p vsebujejo številke pravilno rešenih korakov pri vsaki nalogi (kakor so označeni v rešitvah), stolpci n1, n2 in n3 pa število doseženih točk pri posamezni nalogi. Skupno število točk doseženih na 2. ali 3. pisnem izpitu v stolpcu i2 oziroma i3 je najprej pomnoženo z 2 in nato zapisano v stolpec “vsota”, na podlagi česar je po standardnem kriteriju določena ocena. Če je tako dobljena vsota boljša kot vsota po 1.A in 1.B pisnem izpitu ali po 2. pisnem izpitu, je skupaj z oceno označena z modro barvo.

Ker s 3. pisnim izpitom zaključujemo študijsko leto, vsem želim veliko uspehov tudi v prihodnosti.

– Martin Klanjšek

(23. 8. 2022)

Napoved 3. PISNEGA IZPITA iz vaj

3. in s tem zadnji pisni izpit iz vaj bomo pisali v petek, 1. 9. 2023, s pričetkom ob 10:00 v predavalnici F1. Izpit bo vseboval tri naloge, čas reševanja bo 90 minut. V poštev pride vsa snov. Na izpitu bo dovoljeno uporabljati

1) spisek enačb dostopen kot priponka eno novico pod napovedjo 1.B pisnega izpita (potrebno si ga je natisniti, nekaj kopij bom imel s sabo za vsak slučaj),

2) matematični priročnik in

3) kalkulator.

Katera ocena OBVELJA? Že pridobljene ocene (na 1.A in 1.B ali na 2. pisnem izpitu) z udeležbo na 3. pisnem izpitu ni mogoče pokvariti. Obvelja boljša ocena.

PRIJAVA na izpit. Vse, ki se nameravate izpita udeležiti, prosim, da svojo udeležbo napoveste na tej povezavi v spletni učilnici. Vnaprejšnje poznavanje predvidene udeležbe mi bo omogočilo, da se bom lahko primerno organiziral in po pisnem izpitu čimprej pregledal rešitve vseh udeležencev.

– Martin Klanjšek

(7. 2. 2023)

2. pisni izpit: naloge, REŠITVE in REZULTATI

Zaradi bližajočega se roka za ustni izpit sem oddane rešitve pregledal karseda hitro. V priloženih dokumentih objavljam naloge, rešitve nalog (s točkovalnikom) in tabelo rezultatov2. pisnega izpita skupaj z ocenami po 2. pisnem izpitu. Kot ponavadi, stolpci n1p, n2p in n3p vsebujejo številke pravilno rešenih korakov pri vsaki nalogi (kakor so označeni v rešitvah), stolpci n1, n2 in n3 pa število doseženih točk pri posamezni nalogi. Podatek o pravilno rešenih korakih naj bi ob fotografijah oddanih rešitev vsakomur omogočil, da bo čim bolje razumel število dodeljenih točk. Skupno število točk doseženih na 2. pisnem izpitu v stolpcu i2 je najprej pomnoženo z 2 in nato zapisano v stolpec “vsota”, na podlagi česar je po standardnem kriteriju določena ocena. Če je tako dobljena vsota boljša kot vsota po 1.A in 1.B pisnem izpitu, je skupaj z oceno označena z rdečo barvo.

Kot ponavadi sem ocenjeval dokaj prizanesljivo. Le delno pravilni koraki, ki pa sem jih točkovno v celoti priznal, so označeni v oklepaju. V glavnem sem to naredil zaradi manjkajočih točk do višje ocene, kjer sem občasno tudi podaril kakšno osminko točke, če drugače ni šlo.

Kdor ima občutek, da sem ga ocenil narobe, naj mi prosim piše na mojelektronski naslov.

Ker z 2. pisnim izpitom zaključujemo semester, vsem želim veliko uspehov tudi v prihodnosti.

3. pisni izpit bo v petek, 1. 9. 2023 ob 10:00 v predavalnici F1. Obvestilo o izpitu bom objavil sredi avgusta.

– Martin Klanjšek

(27. 1. 2023)

NAPOVED 2. pisnega izpita

2. pisni izpit iz vaj bomo pisali v petek, 3. 2. 2023, s pričetkom ob 13:00 v predavalnici VFP. Izpit bo vseboval tri naloge, čas reševanja bo 90 minut. V poštev pride vsa snov. Na izpitu bo dovoljeno uporabljati

1) spisek enačb dostopen na spodnji povezavi (potrebno si ga je natisniti, nekaj kopij bom imel s sabo za vsak slučaj),

2) matematični priročnik in

3) kalkulator.

Katera ocena OBVELJA? Že pridobljene ocene (na 1.A in 1.B pisnem izpitu) z udeležbo na 2. pisnem izpitu ni mogoče pokvariti. Obvelja boljša ocena.

PRIJAVA na izpit. Vse, ki se nameravate izpita udeležiti, prosim, da svojo udeležbo napoveste na tej povezavi v spletni učilnici.

– Martin Klanjšek

(27. 1. 2023)

1.B pisni izpit: naloge, REŠITVE in REZULTATI

V priloženih dokumentih objavljam naloge, rešitve nalog (s točkovalnikom) in tabelo rezultatov1.B pisnega izpita skupaj z ocenami po 1.A in 1.B pisnem izpitu. Zelo me veseli, da ste tisti, ki ste se udeležili 1.B pisnega izpita, v veliki večini lepo izkoristili vnaprej napovedano dejstvo o nekoliko lažjih nalogah. Rezultati so namreč zelo dobri.

Tabela rezultatov je urejena na naslednji način:

– v prvem stolpcu (vpisna) je vpisna številka sodelujočega,

– v drugem stolpcu (i1A) je dosežek 1.A pisnega izpita,

– v naslednjih treh stolpcih (n1p, n2p, n3p) so navedeni pravilno rešeni koraki pri vsaki nalogi (oštevilčeni od 1 do 8, kakor v rešitvah, vsak vreden 1/8 = 0.125 točke),

– v naslednjih treh stolpcih (n1, n2, n3) je navedeno število doseženih točk pri vsaki nalogi,

– v naslednjem stolpcu (i1B) je vsota doseženih točk na 1.B pisnem izpitu,

– v zadnjih dveh stolpcih pa sta skupna vsota doseženih točk (vsota) in ustrezna ocena (ocena).

Podatek o pravilno rešenih korakih naj bi ob fotografijah oddanih rešitev vsakomur omogočil, da bo čim bolje razumel število dodeljenih točk.

Kot ponavadi sem ocenjeval razmeroma prizanesljivo. Le delno pravilni koraki, ki pa sem jih točkovno v celoti priznal, so označeni v oklepaju. V glavnem sem to naredil zaradi manjkajočih točk do višje ocene, kjer sem občasno tudi podaril osminko točke, če drugače ni šlo. Kdor ima občutek, da sem ga ocenil narobe, naj mi prosim piše na moj elektronski naslov.

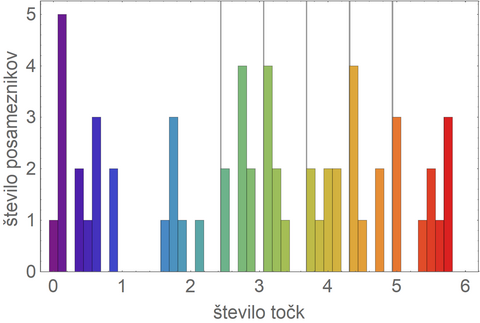
Spet sem naredil primerjavo z rezultati po 1.B pisnem izpitu (oziroma 2. kolokviju) v letih med 2019 in 2022. Zdaj je povprečno število doseženih točk po 1.A in 1.B pisnem izpitu znašalo 3.0 točke (pri čemer so upoštevane tudi ničle tistih, ki niso prišli na 1.B pisni izpit), kar je čisto primerljivo z razponom med 3.0 in 3.1 v preteklosti. Nekoliko lažji 1.B pisni izpit je torej pomagal dvigniti povprečje doseženih točk na običajno raven. Spodaj objavljam tudi histogram števila doseženih točk po 1.A in 1.B pisnem izpitu. Navpične črte označujejo meje za posamezne ocene. Tik pod vsako mejo je lepo vidna praznina. 🙂

V kratkem bom objavil tudi napoved 2. pisnega izpita.

– Martin Klanjšek

(12. 1. 2023)

PRIJAVA na 1.B pisni izpit (2. kolokvij)

Vse, ki se nameravate udeležiti 1.B pisnega izpita (po starem 2. kolokvija), ki bo v petek, 20. 1. 2023, ob 10:00 v VFP, prosim, če lahko to potrdite v spletni učilnici na tejle povezavi. Na ta način bom dobil občutek, koliko vas bo, da bom lahko pripravil ustrezno število kopij s teksti nalog.

Vnaprej hvala!

– Martin Klanjšek

(17. 1. 2023)

Sproti osvežena zbirka nalog do vključno zadnjih, 14. vaj

Na spodnji povezavi objavljam vedno znova osveženo zbirko nalog, ki jih rešujemo na vajah. Zbirko osvežujem vsak ponedeljek popoldne ali torek dopoldne, se pravi pred torkovimi vajami. Nove naloge dodajam na koncu dokumenta.

– Martin Klanjšek

(12. 1. 2023)

NAPOVED 1.B pisnega izpita (2. kolokvija)

V petek, 20. 1. 2023 bomo v predavalnici VFP pisali 1.B pisni izpit (po starem 2. kolokvij), in sicer s pričetkom ob 10:00. V poštev pride snov od vključno 8. vaj (se pravi od vključno 18. naloge) pa do konca. Izpit bo vseboval tri naloge, čas reševanja pa bo 90 minut. Na izpitu bo dovoljeno uporabljati:

1) spisek enačb dostopen na spodnji povezavi (natisnite si ga sami, s sabo pa bom za vsak slučaj imel nekaj kopij),

2) matematični priročnik,

3) kalkulator.

Besedila nalog praviloma vsebujejo tudi za reševanje potrebne “matematične pripomočke”, kot so splošne rešitve Laplaceovih enačb, zahtevnejši integrali, zapis vektorskih operatorjev v raznih koordinatah, ničle Besslovih funkcij itd.

Vzpodbuda: 1.B pisni izpit je vedno nekoliko lažji od 1.A pisnega izpita, tokrat pa bo še zlasti tako. Vsem res priporočam, da se potrudite. Običajno je kriterij po 1.A in 1.B pisnem izpitu takšen, da je za pozitivno oceno potrebno skupaj zbrati 2.5 točke, za najvišjo oceno pa 5 točk (od skupno 6 možnih).

– Martin Klanjšek

(17. 1. 2023)

Zgodbe iz aktualne fizike

Tole je seznam petminutnih zgodb o nedavnih pomembnih odkritjih v fiziki (predvsem z mojega področja fizike kondenzirane snovi in kvantnih materialov), ki jih pripovedujem na začetku vsakih vaj. Vsaka zgodba je opremljena z ustrezno referenco oziroma referencami.

1) Napoved letošnje Nobelove nagrade iz fizike, ki bi jo lahko prejeli Aspect, Clauser in Zeilinger za eksperimentalno potrditev kvantne prepletenosti, ki je osnova kvantne fizike in nastajajočega področja kvantne informatike. Ker se je dobro uro zatem izkazalo, da je napoved končno uresničena, je gradiva tokrat nekoliko več: Announcement of the 2022 Nobel Prize in Physics, How entanglement has become a powerful tool, Scientific Background on the Nobel Prize in Physics 2022.

2) Frakcijski kvazidelci z nabojem, ki je le del osnovnega naboja, so bili prvič zaznani v okviru frakcijskega kvantnega Hallovega pojava, za odkritje katerega je bila podeljena Nobelova nagrada iz fizike leta 1988. Pred kratkim so ugotovili, da so eksperimentalni znaki frakcijskih kvazidelcev v električnem šumu še mnogo bolj univerzalni, kot je kazalo doslej: Noisy fractions.

3) Visokotemperaturno superprevodnost, ki v nekaterih kupratih preživi celo do 150 K, so odkrili leta 1986, za kar je bila leta 1987 podeljena Nobelova nagrada iz fizike. Medtem ko v standardnih superprevodnikih nihanja kristalne mreže omogočijo, da se elektroni sparijo, kar vodi do superprevodnosti, pa mehanizem parjenja elektronov v kupratih ostaja uganka. Nedavni eksperiment najprepričljiveje doslej kaže, da je ta mehanizem superizmenjalna magnetna interakcija med spini elektronov: High-Temperature Superconductivity Understood at Last.

4) Kvantni računalniki, katerih delovanje temelji na kvantnih bitih oziroma kubitih, imajo težavo, da stanja kubitov zaradi motenj iz okolice, segrevanja in nenadzorovanih interakcij s časom počasi razpadejo. Znano je, da stalno vzbujanje kubitov s periodičnimi laserskimi sunki pomaga pri dolgoživosti kubitov. Nedavni eksperiment pa kaže, da so pri tem še uspešnejši kvaziperiodični laserski sunki, katerih oblika je povezana s Fibonaccijevim zaporedjem: Strange new phase of matter created in quantum computer acts like it has two time dimensions.

5) Ramanov pojav je neelastično sipanje vidne svetlobe na nihajočih in vrtečih se molekulah v snovi. Raman se je iskanja tega pojava pri vidni svetlobi lotil po zgledu tik pred tem odkritega Comptonovega pojava, se pravi neelastičnega sipanja rentgenskih žarkov na prevodniških elektronih v snovi. Za odkritje Ramanovega pojava je Raman leta 1930 prejel Nobelovo nagrado iz fizike. Ramanovo zanimanje za sipanje vidne svetlobe pa izvira iz njegove rešitve preproste uganke, in sicer zakaj je morje modro: Raman scattering discovered.

6) Sinhronizacijo sklopljenih nihal je prvi popisal Huygens davnega leta 1665. Opazil je namreč, da se nihajni uri, obešeni na isto steno, a zanihani v različnih fazah, sčasoma sinhronizirata, tako da nihata v fazi. Pojav je mogoče opazovati tudi v skupinah nekaterih vrst kresnic, ki v azijskih gozdovih utripajo povsem usklajeno. Pri tem je ključna sklopitev med posameznimi “nihali”, ki sčasoma privede do sinhronizacije. Pred kratkim pa so pri vrsti ameriške kresnice opazili in razložili malce drugačno vrsto sinhronizacije, kjer je periodično ponavljajočege se utripanje povsem emergenten pojav, ki ga ena sama kresnica ne kaže: How Do Fireflies Flash in Sync? Studies Suggest a New Answer.

7) Moebiusov trak dobimo, če papirnati trak sklenemo tako, da en konec pred tem zasukamo za pol obrata. Tako dobljena ploskev ima samo eno stran, v določeno točko pa se lahko vrnemo šele, če vzdolž traku opravimo pot dvakratne dolžine traku. Pred kratkim so uspeli izdelati Moebiusov trak za svetlobo, se pravi majhen krožni valovni vodnik, po katerem mora svetloba opraviti dva obrata, da se vrne v isto stanje. Trik je v enakomerno razporejenih zarezah vzdolž vodnika, ki pa jih je liho mnogo: A Moebius Strip for Light.

8) Cabrerov eksperiment je z uporabo superprevodne krožne zanke poskusil zaznati proste magnetne monopole. Če namreč monopol prečka ravnino zanke, v njej inducira električni tok, ki v zanki ostane. Nasprotno pa magnetni dipol inducira le sunek električnega toka. V eksperimentu so v petih mesecih opazovanja zaznali natanko eno domnevno prečkanje magnetnega monopola, ki je hkrati vodil do pričakovane vrednosti električnega toka v skladu z Diracovo kvantizacijo: First Results from a Superconductive Detector for Moving Magnetic Monopoles. A ker kasnejši podobni eksperimenti takšnega dogodka niso več zaznali, Cabrerov eksperiment ne velja za ponovljivega, tako da obstoj prostih magnetnih monopolov ni dokazan.

9) Spinski led označuje skupino magnetnih snovi, katerih struktura je enaka strukturi vodnega ledu, pri čemer se v ogliščih strukturnih tetraedrov nahajajo magnetni spini. Smer vsakega spina je omejena na premico skozi središče ustreznega tetraedra, tako da spin lahko kaže le proti središču tetraedra (noter) ali stran od njega (ven). V osnovnem stanju spinskega ledu pri nizkih temperaturah za vsak tetraeder velja, da dva spina kažeta noter, dva pa ven, kar efektivno ustreza ničelni divergenci magnetnega polja v središču tetraedra. Če en spin prekucnemo, divergenca v sosednjih tetraedrih, ki si delita ta spin, postane neničelna, kar pomeni, da smo v njiju vzbudili dva magnetna monopola nasprotnih predznakov: Magnetic monopoles in spin ice. Številni eksperimenti kažejo, da je spinski led odličen laboratorij za magnetne monopole.

10) Alexei Kitaev je leta 2006 proučil model kvantnih spinov na mreži satovja, kjer so pari najbližjih spinov sklopljeni z Isingovo interakcijo, ki ima različne osi za tri različne smeri vezi. Pokazal je, da je natančno osnovno stanje takšnega modela kvantna spinska tekočina, v kateri se osnovne vzbuditve ne obnašajo niti kot fermioni niti kot bozoni, pač pa kot nekaj vmes, čemur je Nobelovec Frank Wilczek nadel ime anyoni. Kitaev je pokazal tudi, da posebna vozlasta narava anyonov omogoča, da bi jih lahko uporabili za kvantno računalništvo. Za najboljšo realizacijo modela Kitaeva trenutno velja kristal RuCl₃, ki se ga v zadnjih sedmih letih intenzivno proučuje in v katerem so različne skupine (vključno z mojo) zaznale znake navzočnosti omenjenih anyonov: Concept and realization of Kitaev quantum spin liquids.

11) Bose-Einsteinova kondenzacija svetlobe je kolektivna kondenzacija kvantov svetlobe, se pravi fotonov, v osnovno kvantno stanje. Ker imajo fotoni spin ena, so bozoni in jih je zato načeloma mogoče kondenzirati. Težava je v tem, da so fotoni v običajnih okoliščinah brez mase, tako da v kondenziranem stanju izginejo. Leta 2010 je raziskovalcem uspelo uresničiti trik, s katerim so fotonom naredili neničelno maso, in sicer tako, da so jih omejili na resonator, napolnjen z barvilom s primernimi absorpcijskimi lastnostmi. Posledično so uspeli pripraviti kondenzat fotonov, ki je seval koherentno svetlobo, podobno kot laser: Bose–Einstein condensation of photons in an optical microcavity.

12) Fraktali so geometrijske oblike s podrobno strukturo na poljubno majhnih skalah. Prav zato imajo večjo dimenzijo od dimenzije sestavnih geometrijskih elementov, pogosto pa so si podobni na različnih skalah. V naravi poznamo kar nekaj primerov fraktalnih struktur, še najbolj znan primer je brokoli romanesco. Pred kratkim pa so odkrili prvi dinamični fraktal, in sicer v posebni vrsti magnetov s skupnim imenom spinski led: Dynamical fractal and anomalous noise in a clean magnetic crystal. Osnovne magnetne vzbuditve v spinskem ledu so magnetni monopoli, ki se lahko po snovi gibljejo zaradi prekucevanja posameznih spinov. Sled posameznega monopola tako omeji povsem prosto gibanje preostalih monopolov, zaradi česar so ti omejeni samo na fraktalni del celotnega prostora spinskega ledu. Prav ta pojav pa je odgovoren za doslej še nepojasnjeno frekvenčno odvisnost magnetnega šuma v spinskem ledu.

13) Vrteča harmonikasta cev oziroma “whirly tube” je zanimiv glasbeni instrument. Uporabljamo jo tako, da jo držimo za en konec in jo vrtimo, tako da drugi konec opisuje krožnico. Nihanje zraka, ki pri tem nastane v cevi, povzroči zvok z jasno določeno resonančno frekvenco cevi kot piščali. Pri hitrejšem vrtenju cevi v njej vzbudimo zvok z višjo frekvenco, ki je harmonik (oziroma večkratnik) osnovne frekvence. V predavalnici smo s telefonsko aplikacijo phyphox izmerili prve štiri frekvence zvoka in ugotovili, da druga ni dvakratnik prve, pač pa le 1.5-kratnik. Razlog je v tem, da prva izmerjena frekevnca ni osnovna, pač pa že drugi harmonik. Zvok z osnovno frekvenco je namreč zelo težko vzbuditi, saj je njegova glasnost zelo majhna.

– Martin Klanjšek

(5. 12. 2022)

1.A pisni izpit: naloge, REŠITVE in REZULTATI

V priloženih dokumentih objavljam naloge, rešitve nalog (s točkovalnikom) in tabelo rezultatov 1.A pisnega izpita. Tabela je urejena na naslednji način:

– v prvem stolpcu je vpisna številka sodelujočega,

– v naslednjih treh stolpcih (n1p, n2p, n3p) so navedeni pravilno rešeni koraki pri vsaki nalogi (oštevilčeni od 1 do 8, kakor v rešitvah, vsak vreden 1/8 = 0.125 točke),

– v naslednjih treh stolpcih (n1, n2, n3) je navedeno število doseženih točk pri vsaki nalogi,

– v zadnjem stolpcu pa je vsota doseženih točk z odebeljeno pisavo.

Podatek o pravilno rešenih korakih naj bi ob fotografijah oddanih rešitev vsakomur omogočil, da bo čim bolje razumel število dodeljenih točk.

Ocenjeval sem prizanesljivo. Le delno pravilni koraki, ki pa sem jih točkovno v celoti priznal, so označeni v oklepaju. Kdor ima občutek, da sem ga ocenil narobe, naj mi prosim piše na moj elektronski naslov.

Povprečno število doseženih točk na 1.A pisnem izpitu tokrat znaša okoli 1.3 točke, kar je nekoliko manj kot v prejšnjih letih, ko je bila ta vrednost nekaj pod 1.6 točke. Razlog za nižje povprečje je v nenavadni obliki porazdelitve števila doseženih točk (na spodnjem histogramu), ki ima razmeroma veliko gostoto pri nizkem številu točk (pod 1), čeprav je hkrati posameznikov z velikim številom točk (vsaj 2.5) relativno celo nekaj več kot prejšnja leta. Težko je reči, zakaj je prišlo do tega, a zdi se mi, da razlog ni v večji težavnosti nalog. Skupna težavnost je bila tokrat podobna kot v prejšnjih letih. Druga naloga je bila skoraj enaka kot na vajah, prva je bila malce zapletenejša verzija naloge z vaj, tretja pa je bila edina, pri kateri je bilo treba malo več razmišljati. Kdor je redno hodil na vaje in jim sledil, ne bi smel imeti težave zbrati vsaj 1.5 točke. Sem pa vse od 3. vaj opažal postopen usip števila obiskovalcev pri vajah, kar je gotovo eden izmed razlogov za nekoliko slabši skupni uspeh. Vsem tistim, ki ste nehali obiskovati vaje, svetujem, da se jim v prihodnosti spet pridružite.

– Martin Klanjšek

(17. 11. 2022)

PRIJAVA na 1.A pisni izpit (1. kolokvij)

Vse, ki se nameravate udeležiti 1.A pisnega izpita (po starem 1. kolokvija), ki bo v petek, 25. 11. 2022, ob 14. uri v VFP, prosim, če lahko to potrdite v spletni učilnici na tejle povezavi. Na ta način bom dobil občutek, koliko vas bo, da bom lahko pripravil ustrezno število kopij s teksti nalog.

Vnaprej hvala!

– Martin Klanjšek

(17. 11. 2022)

NAPOVED 1.A pisnega izpita (1. kolokvija)

V petek, 25. 11. 2022 bomo v predavalnici VFP pisali 1.A pisni izpit (po starem 1. kolokvij), in sicer s pričetkom ob 14:00. V poštev pride snov do vključno 7. vaj, ki jih bomo imeli prihodnji teden. Izpit bo vseboval tri naloge, čas reševanja pa bo 90 minut. Na izpitu bo dovoljeno uporabljati:

1) spisek enačb dostopen na spodnji povezavi (natisnite si ga sami, s sabo pa bom za vsak slučaj imel nekaj kopij),

2) matematični priročnik,

3) kalkulator.

Besedila nalog praviloma vsebujejo tudi za reševanje potrebne “matematične pripomočke”, kot so splošne rešitve Laplaceovih enačb, zahtevnejši integrali, zapis vektorskih operatorjev v raznih koordinatah itd.

– Martin Klanjšek

(27. 10. 2022)

Vaje prihodnji teden odpadejo

Prihodnji teden bo v torek, 1. 11. 2022, državni praznik, tako da bodo vaje v “torkovi skupini” na ta dan odpadle. Da bo za vse veljalo enako, smo se danes v “četrtkovi skupini” domenili, da bodo odpadle tudi vaje v četrtek, 3. 11. 2022. Odpadle vaje bomo nadomestili v torek, 17. 1. 2023 (to je na zadnji dan zimskega semestra), ko bomo torej združili obe skupini.

– Martin Klanjšek

(18. 10. 2022)

Določeni TERMINI PISNIH IZPITOV iz vaj

V preteklih dveh tednih so potekala usklajevanja terminov, tako da imamo končno določene vse termine pisnih preverjanj znanja:

1.A pisni izpit (1. kolokvij): petek, 25. 11. 2022 ob 14:00 v predavalnici VFP,

1.B pisni izpit (2. kolokvij): petek, 20. 1. 2023 ob 10:00 v predavalnici VFP,

2. pisni izpit: petek, 3. 2. 2023 ob 13:00 v predavalnici VFP,

3. pisni izpit: petek, 1. 9. 2023 ob 10:00 v predavalnici F1.

Še pojasnilo glede poimenovanj pisnih preverjanj. Ker dva kolokvija že omogočata pridobitev ocene iz vaj, skupaj tvorita 1. pisni izpit (A in B), sledita pa še 2. in 3. pisni izpit.

– Martin Klanjšek

(4. 10. 2022)

Naloge in rešitve nalog s kolokvijev in izpitov prejšnjih let

Naloge in rešitve nalog so objavljene na naslednjih povezavah, vsakič kot seznam povezav na vrhu strani:

• EMP 2013/2014
• EMP 2014/2015
• EMP 2015/2016
• EMP 2016/2017
• EMP 2017/2018
• EMP 2018/2019
• EMP 2019/2020
• EMP 2020/2021
• EMP 2021/2022

Skupaj gre za zbirko več kot 130 nalog z rešitvami, ki jo priporočam kot pripomoček pri pripravljanju na prihajajoče pisne izpite iz vaj. V primeru kakršnihkoli vprašanj glede nalog sem na voljo, bodisi v živo v odmoru med vajami ali po njih bodisi preko e-pošte.

– Martin Klanjšek

(29. 9. 2022)

Vaje iz EMP v študijskem letu 2022/2023

Pozdrav vsem novim obiskovalcem te spletne strani! V študijskem letu 2022/2023 bodo vaje iz EMP potekale na običajen način, se praviv živo. Zaradi večjega števila obiskovalcev bodo, kot vedno v zadnjih letih, organizirane v dveh skupinah, in sicer:

1) ob torkih od 10:15 do 12:00 v predavalnici F2 ter

2) ob četrtkih od 10:15 do 12:00 v predavalnici F4.

Obe skupini vaj bom vodil jaz, program v obeh skupinah pa bo popolnoma enak. Vsakdo si lahko poljubno izbere skupino, je pa zaradi lažjega spremljanja vaj priporočljivo, da se enakomerno razporedite po obeh skupinah.

Lep pozdrav in se kmalu vidimo!

– Martin Klanjšek